James Evans
 
Director, Program in Science, Technology and Society,
and Professor of Physics, University of Puget Sound.

Associate Editor, Journal for the History of Astronomy.
 

Department of Physics                                                                          Phone:   (253) 879-3813
University of Puget Sound                                                                     Fax:       (253) 879-1572 
1500 North Warner St.
Tacoma, WA 98416  USA                                                                    e-mail: jcevans@ups.edu

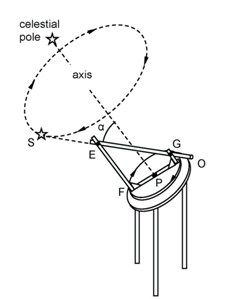
Sundial and analemma in Harned Hall, University of
Puget Sound, designed and installed in 2006.  A mirror
under a skylight reflects a spot of sunlight onto the
sundial and analemma.

Details of sundial and analemma

Equinox slide show (Spring equinox of March 20, 2007,
photographed by Bernard Bates)

Teaching Interests

Courses taught in the last few years include:

PHYS 299  The History and Practice of Ancient Astronomy
STS 166     Science and Theater
STS 201     Introduction to Science, Technology and Society I  (Antiquity to 1800)
STS 202     Introduction to Science, Technology and Society II  (19th and 20th Centuries)
STS 314     Cosmological Thought
STS 348     Strange Realities:  Physics in the Twentieth Century
STS 490     Senior Seminar in STS
HON 212    Origins of the Modern Worldview
PHYS 494  Special Topics in Theoretical Physics:  Variational Principles in Physics

Research Interests

In history of science:  ancient Greek astronomy, science in the Enlightenment,
history of physics from the 18th through the 20th centuries,
history of cosmology from antiquity to the present

In physics proper:  the action principle, optical-mechanical analogies

Books

James Evans, The History and Practice of Ancient Astronomy
(New York: Oxford University Press, 1998)    errata

James Evans and Alan S. Thorndike, eds., Quantum Mechanics at the Crossroads: 
New Perspectives from History, Philosophy and Physics
(Heidelberg: Springer, 2006)

James Evans and J. Lennart Berggren, Geminos's Introduction to the Phenomena:
A Translation and Study of a Hellenistic Survey of Astronomy
(Princeton: Princeton University Press, 2006)   errata

Selected Articles:  History of Science (by James Evans unless co-authors are listed)

“Fonction et origine probable du point équant de Ptolémée.”  Revue d'histoire des sciences et de leurs applications 37 (1984) 193-213.

“On the function and the probable origin of Ptolemy’s equant.” American Journal of Physics 52 (1984) 1080-1089.  pdf

James Evans and Brian Popp, “Pictet’s experiment:  The apparent radiation and reflection of cold.”  American Journal of Physics 53 (1985) 737-753.  pdf

“On the Origin of the Ptolemaic Star Catalogue:  Part 1.”  Journal for the History of Astronomy 18 (1987) 155-172 and “… Part 2,” Journal for the History of Astronomy 18 (1987) 233-278.

“The division of the Martian eccentricity from Hipparchos to Kepler:  A history of the approximations to Kepler motion.”  American Journal of Physics 56 (1988) 1009-1024.  pdf

Articles on ancient Greek astronomy in Encyclopedia of Cosmology, Norriss Hetherington, ed. (New York: Garland Publishing, 1993): “Ptolemaic Planetary Theory,” p. 513-526.  “Ptolemy,” p. 526-528.  “Ptolemy’s Cosmology,” p. 528-544.  “Theon of Smyrna,” p. 642-643.

“A Cosmogenesis: The Origins of Ptolemy’s Universe.”  Histoire et actualité de la cosmologie, Vol. I, François De Gandt and Christiane Vilain, eds.  (Paris: Observatoire de Paris, 1996), p. 21-39.

“Fraud and Illusion in the Anti-Newtonian Rear Guard:  The Coultaud-Mercier Affair and Bertier’s Experiments, 1767-1777.”  Isis 87 (1996) 74-107.  pdf

“The Material Culture of Greek Astronomy.”  Journal for the History of Astronomy 30 (1999) 237-307.  Download from NASA Astrophysics Data System.

“Concetti generali di materia e moto.” Storia della scienza, Sandro Petruccioli, ed., Vol. VI, L’Età dei lumi (Roma: Instituto della Enciclopedia Italiana, 2002), p. 29-42, 46-47. 

Articles on eighteenth-century astronomy in Storia della scienza, Sandro Petruccioli, ed., Vol. VI, L’Età dei lumi (Roma: Instituto della Enciclopedia Italiana, 2002):  “La vecchia guardia e la stabilità del Sistema solare,” p. 244-247.  “Un nuovo Sistema solare,” p. 247-250.  “Il dibattito sulle meteore,” p. 250-252.  “Il movimente del Sole,” p. 252.  “La nuova astronomia fisica,” p. 252-253.  “Longitudine e navigazione,” p. 254-257.  “La luce del Sole,” p. 258-259.  “Nuove istituzioni,” p. 260-261.

“Gravity in the Century of Light:  Sources, Construction and Reception of Le Sage’s Theory of Gravitation.”  Pushing Gravity:  New Perspectives on Le Sage’s Theory of Gravitation, Matthew Edwards, ed. (Montreal: Apeiron, 2002), p. 9-40.

“The Origins of Ptolemy’s Cosmos.” Cosmology through Time: Ancient and Modern Cosmologies in the Mediterranean Area, S. Colafrancesco and G. Giobbi, eds. (Milano: Mimesis 2003), p. 123-132.

“The Astrologer’s Apparatus:  A Picture of Professional Practice in Greco-Roman Egypt.”  Journal for the History of Astronomy 35 (2004) 1-44. Download from NASA ADS.

“Gnōmonikē Technē: The Dialer’s Art and Its Meanings for the Ancient World.”  The New Astronomy: Opening the Electromagnetic Window and Expanding our View of Planet Earth, Wayne Orchiston, ed. (New York: Springer, 2005), p. 273-292.

"Equating the Sun: Geometry, Models, and Practical Computing in Greek Astronomy."  Hands On History: A Resource for Teaching Mathematics, Amy Shell-Gellasch, ed. (Washington, D.C.: Mathematical Association of America, 2007), p. 115-123.

James Evans and Marcel Marée, “A Miniature Ivory Sundial with Equinox Indicator from Ptolemaic Tanis, Egypt." Journal for the History of Astronomy 39 (2008) 1-17.  pdf

James Evans, Christian C. Carman, and  Alan S. Thorndike, "Solar Anomaly and Planetary Displays in the Antikythera Mechanism," Journal for the History of Astronomy 41 (2010) 1-39.  pdf

“Astronomy.” The Classical Tradition, ed. by Anthony Grafton, Glenn W. Most, and Salvatore Settis (Cambridge: Harvard University Press, 2010), p. 89-96.

Christian C. Carman, Alan S. Thorndike, and James Evans, "On the Pin-and-Slot Device of the Antikythera Mechanism, with a New Application to the Superior Planets" Journal for the History of Astronomy 43 (2012) 93-116. pdf


Tracking the Cosmos: The Technology of the Antikythera Mechanism.  Video conversation between Jo Marchant, James Evans, and Patt Morrison about the Antikythera Mechanism, at the Getty Villa in 2010. http://www.getty.edu/museum/programs/past_programs/antikythera.html


Historical Picture Gallery

        Vignettes of Space and Time in Emilie du Châtelet's Institutions de physique (1740).
                See “Concetti generali di materia e moto” (2002).

      (Left)     Magical gem of Aphrodite that may have functioned as a planet marker for an astrologer's board in Greek Egypt.
      (Right)  A coin carrying the zodiac sign of Aries, from the Roman mint of Alexandria, year 8 of Antoninus Pius (AD 144/145).
                See “The Astrologer's Apparatus" (2004).

Georges-Louis Le Sage's mechanical explanation of universal gravitation, from his Essai de chymie méchanique(1758).
        See “Gravity in the Century of Light" (2002).
                                                                           

Marc-Auguste Pictet (1722-1825), the maker
of a paradoxical experiment on the radiation 
and reflection of cold. 
        See “Pictet's Experiment" (1985).

(Left)    Mosaic of an armillary sphere at Solunto, near Palermo.  Photo by Rudolf Schmidt.
(Right)  Conjectural reconstruction of Geminos's equatorial dioptra. 
        See Geminos's "Introduction to the Phenomena" (2006).

 

 

 

 

 

 

 

 

Gothic astrolabe of French or Italian workmanship, early 15th century.
        See The History and Practice of Ancient Astronomy.

Clockwise from top left:  Letter from a mysterious Jean Coultaud, describing pendulum
    experiments performed in the mountains, refuting Newton's inverse-square law of gravitation.
Jean-Louis Aubert (1731-1814), editor of the Journal des Beaux-Arts et des Sciences, where
    Coultaud's letter appeared in 1767.
Some hypothetical Earths, from Jean-Pierre David, Dissertation sur la figure de la terre
    (La Haye, 1771).
Church of the Oratory, rue St. Honoré, Paris, where Father Joseph-Étienne Bertier performed
    experiments showing that objects weigh more, the higher up they are located.    
               See "Fraud and Illusion in the Anti-Newtonian Rear Guard" (1996).

Obelisk, taken from Heliopolis in Egypt, and used as gnomon for the monumental sundial set up in Rome by Augustus.  The obelisk is now located in the Piazza di Montecitorio, several hundred feet south of its ancient site.
        See “Gnōmonikē Technē: The Dialer’s Art and Its Meanings for the Ancient World” (2005).

An equatorium for finding the place of the Sun in the zodiac.  The instrument is intended to resemble the back of an astrolabe.  From Cosmographia ... Petri Apiani & Gemmae Frisii (Antwerp, 1584).
        See "Equating the Sun" (2007).

(Left)  The Tower of the Winds in Athens.  Each wall of this octagonal building (constructed around 50 BC) carries a vertical, plane sundial.  From James Stuart and Nicholas Revett, The Antiquities of Athens (London, 1762).  (Below)  A modern copy of the Farnese globe, one of three intact celestial globes to have survived from antiquity.
        See “The Material Culture of Greek Astronomy” (1999). 

(Left)  A conical Greek sundial of the first century B.C.E., found by Flinders Petrie in 1884, but only recently restored.  (Right)  Analysis of the sundial.
        See "A Miniature Ivory Sundial with Equinox Indicator from Ptolemaic Tanis, Egypt" (2008).


 © The British Museum

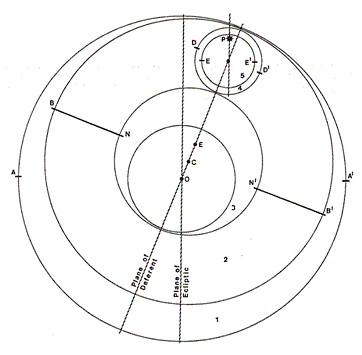
The three-dimensional orbs for Mars, as described in Ptolemy's Planetary Hypotheses.  The earth is at O; the planet is at P.
        See “The Origins of Ptolemy’s Cosmos” (2003).

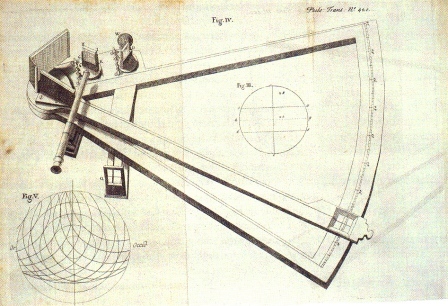
John Hadley's reflecting quadrant.  From "The description of a new instrument for taking angles," Philosophical Transactions (1731).

Selected Articles:  Scientific Papers

James Evans and Mark Rosenquist, “ ‘F = ma’ optics.”  American Journal of Physics 54 (1986) 876-883.  pdf

“Simple forms for equations of rays in gradient-index lenses.”  American Journal of Physics 58 (1990) 773-778.  pdf

James Evans, Kamal K. Nandi and Anwarul Islam, “The Optical-Mechanical Analogy in General Relativity:  Exact Newtonian Forms for the Equations of Motion of Particles and Photons.”  General Relativity and Gravitation 28 (1996) 413-439.  pdf

James Evans, Kamal K. Nandi and Anwarul Islam, “The optical-mechanical analogy in general relativity:  new methods for the paths of light and of the planets.”  American Journal of Physics 64 (1996) 1404-1415.  pdf

Matthew J. Moelter, James Evans, Greg Elliott and Martin Jackson, “Electric potential in the classical Hall effect:  An unusual boundary-value problem.”  American Journal of Physics 66 (1998), 668-677.  pdf

James Evans, Paul M. Alsing, Stefano Giorgetti and Kamal Kanti Nandi, “Matter waves in a gravitational field:  An index of refraction for massive particles in general relativity.”  American Journal of Physics 69 (2001) 1103-1110.  pdf

“The universal Lagrangian for one particle in a potential.”  American Journal of Physics 71 (2003) 457-461.  pdf
 

Some Physics Snapshots

The meaning of the Lagrangian L:  The classical action ∫ L dt is the number of phase waves that pass through the moving particle as the particle moves  from its initial to its final point. Let p represent the momentum; v_p the phase  velocity of the underlying phase waves; and v_g the group velocity (equal to the particle velocity). If p and v_g are in the same direction, the Lagrangian is simply L = p(v_g - v_p). If the momentum and group velocity are not in the same  direction (as may occur when a vector potential is present), the Lagrangian is L = p∙v_g - pv_p. The figure shows phase waves for this latter case characterized by phase velocity v_p and group velocity v_g. 
        See "The universal Lagrangian" (2003).  

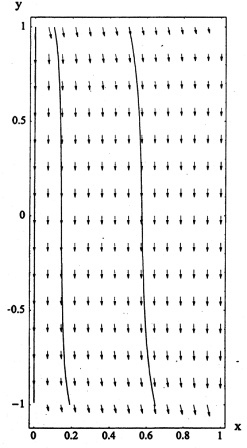
Equipotentials (left) and current density (right) in a metal plate for a  Hall effect experiment.  Potentials of +1 v and -1 v are applied at the top and bottom edges of the plate. A uniform magnetic field is into the plane. This electrostatic potential problem provides a simple but surprisingly rich example of a non-standard boundary-value problem. That is, the natural boundary conditions are not of Dirichlet, Neumann, or of mixed Dirichlet and Neumann type. The resulting family of basis functions are not all orthogonal in pairs; a special technique is  therefore required for constructing a solution.  
        See "Electric potential in the classical Hall effect: 
        An unusual boundary-value problem" (1998).