PENGUIN (Neshyba, Rowe, & Rivers, 2023)

Warming of an ice-free Arctic

Introduction

Over the last few decades, the temperature of the Arctic region has been rising fast -- at a rate of about 1 degree per decade (see https://climate.copernicus.eu/esotc/2020/arctic-temperatures). That's as much as four times faster than the rest of the Earth has been warming (see https://www.nature.com/articles/s43247-022-00498-3). This extra warming, called Arctic amplification, is thought to be due primarily to the reduction in the coverage of ice and snow in the Arctic region, over land and sea.

The temperature difference you'll calculate here is all about an additional kind of Arctic amplification due to the complete disappearence of summertime ice and snow over the Arctic Ocean. Arctic amplification due to this mechanism hasn't fully kicked in yet because Arctic sea ice is still present in the summer, but we know it is happening -- you can see the trend in Figs. 1 and 2 below.

Figure 1. The 2015 Arctic sea ice summertime minimum, compared to the 1981-2010 average (from https://www.nbcnews.com/science/environment/rapid-melt-arctic-sea-ice-shrinks-fourth-lowest-level-record-n427866?cid=par-sy-_all).

Figure 2. Seasonal and interannual variation in Arctic sea ice areal extent (from https://zacklabe.com/arctic-sea-ice-extentconcentration/).

Positive feedbacks and climate tipping points

Thinking about the relationship between the disappearance of sea ice and $CO_2$-induced global warming, you might make the following objection: isn't the disappearance of sea ice the result of an increase in temperature due to human emissions of $CO_2$? How can it be both cause and effect? The answer is, $CO_2$-induced warming and sea ice loss feed off one another, known in climate science as a positive feedback between the two processes.

Positive feedbacks are especially worrisome because embedded in them is the idea that at a certain point, these feedback mechanisms might lead to what is called a tipping point. Dynamical systems that experience positive feedback are susceptible to taking on a life of their own. One big worry regarding the Arctic is that it has already passed, or is at least very close to, a tipping point in which summertime Arctic sea ice will go away permanently, and therefore the warming will continue even if humans back off on the $CO_2$ that got the warming started.

There are lots of other ways the climate system could accidentally trigger tipping points when the global temperature rises above $1.5-2$ degrees Celsius -- for further reading, you can check out https://rmets.onlinelibrary.wiley.com/doi/full/10.1002/wea.4058. Avoiding these climate tipping points is a big reason the signers of the Paris Climate Agreement (https://unfccc.int/process-and-meetings/the-paris-agreement) stipulated that we should really, really keep warming under $1.5-2$ degrees Celsius.

The idea of this CGI

This CGI is an exploration of how much the Arctic's temperature would go up as a result of the additional loss of ice and snow in the Arctic Ocean. Figure 3 shows the factors we'll be considering here. The questions we'll be focusing on are: How much additional warming might there be? and How does that compare with the Arctic amplification we've seen so far?

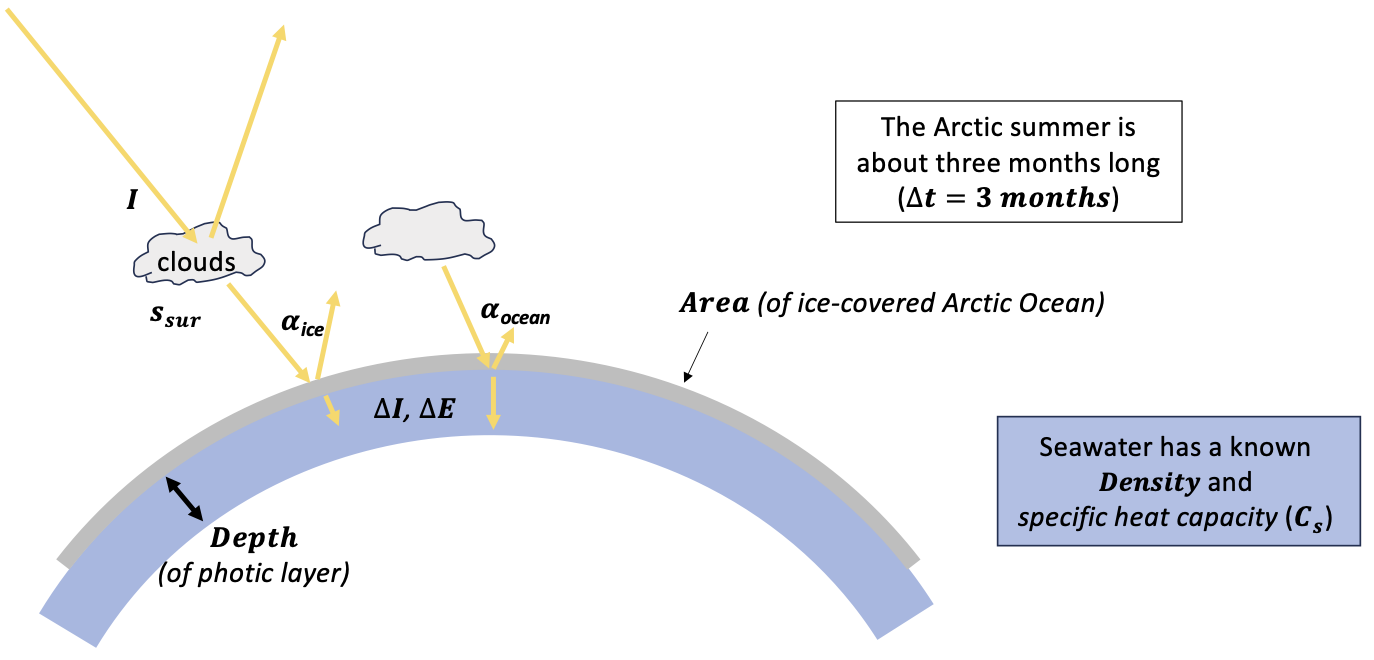Figure 3. Factors influencing the heating effect of loss of summertime Arctic Ocean ice.

Part 1. Heat capacity of the photic layer of the Arctic Ocean

Where to start? You probably have an intuition about this: when you try to heat something up, the more massive it is, the harder it is to heat it up. In our case, we'll need the total mass of the photic layer of the ocean (top 200 meters) of the Arctic Ocean, since that's the layer that will be absorbing most of that additional sunlight once the cover of sea ice is gone.

$$ mass = Area \times Depth \times Density \ \ \ \ (1) $$

Those quantities have been measured -- some by satellite, others in laboratories. Check out these sources for values:

• https://en.wikipedia.org/wiki/Arctic_Ocean
• https://www.noaa.gov/jetstream/ocean/layers-of-ocean
• https://en.wikipedia.org/wiki/Photic_zone
• https://en.wikipedia.org/wiki/Seawater

To get the heat capacity, $C$, of the photic layer, we can use

$$ C = C_s \times mass \ \ \ \ (2) $$

where $C_s$ is called the specific heat capacity of water. That's also a known quantity (see https://en.wikipedia.org/wiki/Table_of_specific_heat_capacities).

Part 2. The insolation impact

We'll also need to know the difference in solar energy getting into the Arctic Ocean when the ice is gone. We can start with how much light is hitting the surface in the first place. That's called the insolation, and symbolized as $I$. Insolation varies with the time of year, and with the latitude, but that's all been worked out -- check out the 8th figure down at http://arctic-news.blogspot.com/2013/06/open-water-in-areas-around-north-pole.html, as an example.

Now, melting ice doesn't change $I$ -- that's controlled by the sun. But melting does change the fraction of $I$ that actually warms the surface. That's because sea ice reflects away a lot more sunlight than the open ocean does. This reflectivity has a special name in climate science: it's called the albedo. Albedos of all kinds of surface types have been measured -- see https://en.wikipedia.org/wiki/Albedo.

One more note about this -- there are clouds above the ocean in the Arctic that also reflect sunlight. What that means is, the sensitivity, $s_{sur}$, of the overall albedo of the Arctic to changes in the surface albedo, is small -- only about 11% (see https://www.mdpi.com/2073-4433/10/1/12).

So in the end, we have a total solar insolation difference given by

$$ \Delta I = (\alpha_{ice} - \alpha_{ocean}) \times Area \times s_{sur} \times I \ \ \ \ (3) $$

where $Area$ is the same as what we've already considered, namely, the areal extent of the Arctic Ocean.

Part 3. The energy impact

Now we're ready to find the energy difference resulting from the extra sunlight being absorbed after the cover of snow and ice is gone. It's given by

$$ \Delta E = \Delta I \times \Delta t \ \ \ \ (4) $$

where $\Delta t$ is the length of time the Arctic Ocean will be ice-free. If we say the entire summer is ice-free, we'd specify $\Delta t \approx 3 $ months.

Part 4. The temperature impact

A pretty straightforward thermodynamic analysis says that the temperature change we can expect when that additional energy is absorbed by the photic layer of the Arctic Ocean will be given by

$$ \Delta T = {\Delta E \over C} \ \ \ \ (5) $$

Background reading

Useful background reading for this activity is https://e360.yale.edu/features/as_arctic_ocean_ice_disappears_global_climate_impacts_intensify_wadhams.

Learning goals

1. I know the months of the year when Arctic sea ice extent is at a maximum and a minimum;
2. I can explain how the following terms relate to climate: positive feedback, albedo, specific heat capacity, insolation, photic layer, Arctic Amplification, and tipping point;
3. Given the mass and specific heat capacity of a substance, I can find its total heat capacity;
4. Given the area and insolation of geographical region (like the Arctic), I can find the region's total insolation; and
5. I can predict how much the Arctic is likely to warm when summertime ice disappears.

import numpy as np
from pint import UnitRegistry; AssignQuantity = UnitRegistry().Quantity

1. Heat capacity of the photic layer of the Arctic Ocean

Your task in the cell below is to calculate the heat capacity of the photic layer of the Arctic ocean. All intermediate values (density, areal extent, etc.) should be assigned as you go along, with units using AssignQuantity, and printed using f-string syntax. For example, the first assignment in the cell below could look something like

density = AssignQuantity(1020,'kg/m^3')

(assuming that's the value you get from https://en.wikipedia.org/wiki/Seawater).

# Use AssignQuantity to assign (and print) a value for the density of sea water
# Reference: https://en.wikipedia.org/wiki/Seawater
### BEGIN SOLUTION
density = AssignQuantity(1020,'kg/m^3')
print(f"Density: {density}")
### END SOLUTION

# Areal extent of the Arctic Ocean
# Reference: https://en.wikipedia.org/wiki/Arctic_Ocean
### BEGIN SOLUTION
Area = AssignQuantity(14e6, 'km**2')
print(f"Area: {Area}")
### END SOLUTION

# Depth of the part of the ocean that will heat up -- the photic layer
# Reference: https://en.wikipedia.org/wiki/Photic_zone
### BEGIN SOLUTION
depth = AssignQuantity(200, 'meter')
print(f"Depth: {depth}")
### END SOLUTION

# Mass of the Arctic photic zone (see Eq. 1 of the Introduction)
### BEGIN SOLUTION
mass = Area * depth * density
mass.ito('kg')
print(f"Mass: {mass}")
### END SOLUTION

# Specific Heat capacity of water
# Reference: https://en.wikipedia.org/wiki/Table_of_specific_heat_capacities (you can use the 25C value)
### BEGIN SOLUTION
c_specific = AssignQuantity(4.18,'joule / gram / K')
print(f"Specific heat capacity: {c_specific}")
### END SOLUTION

# Heat capacity of the entire photic layer of the Arctic (Eq. 2 of the Introduction)
# (You can expect a number on the order of 10^22 joule/kelvin)
### BEGIN SOLUTION
heat_capacity = c_specific * mass
print(f"Heat Capacity: {heat_capacity}")
heat_capacity.ito('joule/K')
print(f"Heat Capacity: {heat_capacity}")
### END SOLUTION

Density: 1020 kilogram / meter ** 3
Area: 14000000.0 kilometer ** 2
Depth: 200 meter
Mass: 2.856e+18 kilogram
Specific heat capacity: 4.18 joule / gram / kelvin
Heat Capacity: 1.193808e+19 joule * kilogram / gram / kelvin
Heat Capacity: 1.193808e+22 joule / kelvin

2. The insolation impact

As previously, you should assign all intermediate values (insolation, etc.) should be assigned with units using AssignQuantity, and printed using f-string syntax.

# Insolation in the Arctic (say, at 90 degrees north, average between the June solstice and the September equinox
# Reference: http://arctic-news.blogspot.com/2013/06/open-water-in-areas-around-north-pole.html
### BEGIN SOLUTION
insolation = AssignQuantity(250, 'W/m^2')
print(f"Insolation per square meter: {insolation}")
### END SOLUTION

# Sensitivity to surface changes because clouds are overhead (i.e., $11%$ as a fraction, so $0.11$)
# Note that this is a dimensionless quantity, so you can simply assign it using something like "s_sur = 0.11"
### BEGIN SOLUTION
s_sur = 0.11
### END SOLUTION

# Albedo of the open ocean -- also a dimensionless quantity
# Reference: check out the "sample albedos" table at https://en.wikipedia.org/wiki/Albedo
### BEGIN SOLUTION
albedo_ocean = 0.06
### END SOLUTION

# Albedo of sea ice ... according to the above reference, this is about 60%, so 0.6 as a fraction
### BEGIN SOLUTION
albedo_ice = 0.6
### END SOLUTION

# Now we can get the insolation difference (Eq. 3 in the Introduction) -- and convert your result into gigawatts
### BEGIN SOLUTION
insolation_difference = (albedo_ice-albedo_ocean) * s_sur * insolation * Area
insolation_difference.ito('gigawatts')
print(f"Insolation difference: {insolation_difference}")
### END SOLUTION

Insolation per square meter: 250 watt / meter ** 2
Insolation difference: 207900.0 gigawatt

Pause for analysis

A gigawatt is a pretty conventional power unit -- for example, the US Grand Coulee dam power station generates about 7 gigawatts of power. But the number you just got is so much bigger than that, that many people have a hard time getting some kind of intuition about it. One approach that some climate scientists have used to bring it to Earth (so to speak) is to compare it to something else that they might have some intuition about. For example, the energy released by the plutonium-239 fission bomb deployed by the US military over the city of Nagasaki in 1945 was almost 100 terajoules (see https://en.wikipedia.org/wiki/Nuclear_weapon_yield).

In the space below, use that figure to calculate the number of those plutonium-239 fission bombs that correspond to the insolation difference you just calculated. Code for something like that could look like the following:

energy_of_one_p239 = AssignQuantity(100, 'terajoules')
nbombs_per_time = insolation_difference/energy_of_one_p239
print(f"nbombs_per_time: {nbombs_per_time}")                   

Your first try might end up with crazy units, however, like "gigawatt / terajoule". If so, you should convert it (using pint, of course) to "1/second", and print it again.

### BEGIN SOLUTION
energy_of_one_p239 = AssignQuantity(100, 'terajoules')
nbombs_per_time = insolation_difference/energy_of_one_p239
print(f"nbombs_per_time: {nbombs_per_time}")                   
nbombs_per_time.ito('1/second')
print(f"nbombs_per_time: {nbombs_per_time}") 
### END SOLUTION

nbombs_per_time: 2079.0 gigawatt / terajoule
nbombs_per_time: 2.079 / second

Pause for analysis

Just to review, the figure you just got is the extra energy that will be absorbed by the Arctic Ocean once the cover of sea ice is gone, in "number of plutonium-239 fission bomb equivalents per second." Is there anything about your result that surprised you? Does it seem especially small, or especially big, for example?

BEGIN SOLUTION

Any reasonable answer is fine, but it seems to the authors of this CGI that it's a lot.

END SOLUTION

3. The energy impact

The $\Delta t$ assigned at the beginning of the cell below assumes three months of ice-free Arctic summer.

# Let's talk about the summer months (late summer/early fall) of ice-free Arctic, so three months
deltat = AssignQuantity(3, 'month')

# Extra energy delivered to the Arctic in that time (Eq. 4) ... convert to terajoules
### BEGIN SOLUTION
energy_difference = insolation_difference * deltat
print(f"Energy dfference: {energy_difference}")
energy_difference.ito('terajoules')
print(f"Energy dfference: {energy_difference}")
### END SOLUTION

Energy dfference: 623700.0 gigawatt * month
Energy dfference: 1640206260.0 terajoule

4. The temperature impact

In the cell below, compute the change in temperature we'd expect from one ice-free Arctic summer (Eq. 5 of the Introduction), and convert to degrees kelvin if it's not that automatically.

# The resulting change in temperature for one summer (Eq. 5) ... convert to kelvin
### BEGIN SOLUTION
deltaT = energy_difference / heat_capacity
deltaT.ito('kelvin')
print(f"Temperature difference: {deltaT}")
### END SOLUTION

Temperature difference: 0.13739280185758515 kelvin

Warming per decade

The number you just got would correspond to the first summer the Arctic goes ice free (for $\Delta t$ months). After another year, it'll warm up that much again. So, how much temperature rise do we expect from this mechansm over a full decade?

This is easy -- just multiply the value of $\Delta T$ you just got by 10, and print the result.

### BEGIN SOLUTION
deltaT_decade = deltaT * 10
print(deltaT_decade)
### END SOLUTION

1.3739280185758516 kelvin

Pause for analysis

In the cell below, offer some perspective. How does the additional heating of the Arctic you just got compare to the heating the Arctic has experienced over the last few decades ($~1^oC$/decade)?

BEGIN SOLUTION

It's even more -- that is, the rate at which the Arctic will heat will more than double.

END SOLUTION

Validating and finishing up

Assuming all this has gone smoothly and a Kernel/Restart & Run All has run without error, don't forget to

1. Close this notebook using the "File/Close and Halt" dropdown menu, and submit it for evaluation.
2. Press the Logout tab of the Home Page